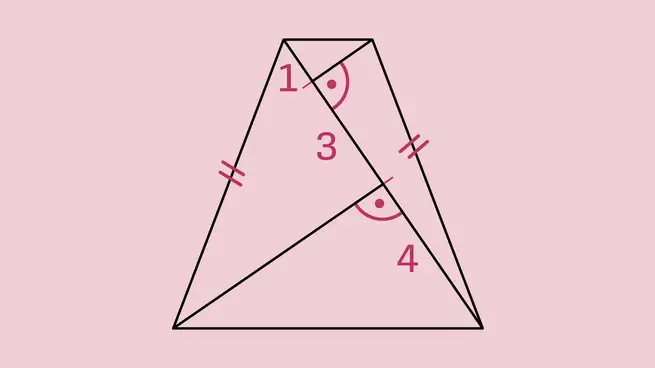Geometrijska zagonetka s trapezom
Dana su tri broja, dva pravokutna kuta i informacija da su dvije strane trapeza jednake duljine – dvije noge s lijeve i desne strane. Dijagram iznad pokazuje pozicije dva pravokutna kuta i tri segmenta s duljinama 1, 3 i 4.
Rješenje zagonetke
Površina trapeza iznosi 20*sqrt(11/5), približno 29.7. Točke trapeza označene su kao A, B, C, D, s točkama E i F na dijagonali. Gledajući označene trokute EDC i ABF, s dijagonalom BD koja sjekne paralelne stranice CD i AB, vidimo da su kutevi EDC i ABF jednaki.
To implicira da su kutevi DCE i BAF također jednaki jer su trokuti oba pravokutna. Stoga su trokuti ABF i EDC slični. S obzirom na da su im kraći bokovi duljine 1 i 4, dulji bokovi su duljine t i 4t (gdje je t nepoznati broj).
Žuti trokut ADF je zrcalna slika trokuta ABF preko segmenta AF, s jednakim unutarnjim kutovima jer su stranice jednake duljine (4 = 1 + 3 i 4t) i kut između stranica je 90 stupnjeva. To znači da je stranica AB jednaka stranici CD i stranici BC.
Sada, pozivajući se na Pitagorin poučak, hipotenuze trokuta EBC i ABF su jednake duljine, što dovodi do jednadžbe (4t)2 + 42 = (3+4)2 + t2. Rješavanjem dobivamo t = sqrt(11/5).
Površina trapeza može biti izračunata koristeći formulu A = 8*(4t + t)/2, rezultirajući A = 20*sqrt(11/5).
Ova matematička zagonetka otkrivena je u Facebook grupi “Geometria Super Top.” Ako ste propustili neke nedavne zagonetke, uključuju zadatke poput rješavanja kutova, brojanja mogućnosti i pronalaženja nedostajućih znamenki.
Za više informacija pročitajte na spiegel